The Art of Linear Algebra

-- Graphic Notes on “Linear Algebra for Everyone" --

作者: Kenji Hiranabe ^[1]

在 Gilbert Strang ^[2] 的亲切帮助下

译者: Kefang Liu ^[3]

日期: September 1, 2021/updated today

摘要

我尝试为 Gilbert Strang 在书籍 “Linear Algebra for Everyone” 中介绍的矩阵的重要概念进行可视化图释, 以促进从矩阵分解的角度对向量、矩阵计算和算法的理解。^[4]它们包括矩阵分解 (Column-Row, $\mathbf{CR}$)、高斯消去法 (Gaussian Elimination, $\mathbf{LU}$)、格拉姆-施密特正交化 (Gram-Schmidt Orthogonalization, $\mathbf{QR}$)、特征值和对角化 (Eigenvalues and Diagonalization, $\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\mathrm{T}}$)、和奇异值分解 (Singular Value Decomposition, $\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}$)。

序言

我很高兴能看到 Kenji Hiranabe 的线性代数中的矩阵运算的图片! 这样的图片是展示代数的绝佳方式. 我们当然可以通过 行 $\cdot$ 列 的点乘来想象矩阵乘法, 但那绝非全部 —— 它是“线性组合”与“秩1矩阵”组成的代数与艺术. 我很感激能看到日文翻译的书籍和 Kenji 的图片中的想法.

-- Gilbert Strang

麻省理工学院数学教授

目录

• 摘要
• 序言
• 目录
• 1、理解矩阵——4个视角
• 2、向量乘以向量——2个视角
• 3、矩阵乘以向量——2个视角
• 4、矩阵乘以矩阵——4个视角
• 5、实用模式
• 6、矩阵的五种分解
  • 6.1
  • 6.2
  • 6.3
  • 6.4
  • 6.5
• 总结和致谢
• 参考文献与相关工作

---

1、理解矩阵——4个视角

一个矩阵 ($m\times n$) 可以被视为$1$个矩阵, $mn$个数, $n$个列和$m$个行。

图 1: 从四个角度理解矩阵

$$A=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\\ a_{31}& a_{32}\end{array}\right]=\left[\begin{array}{cc}|& |\\ {\mathbf{a}}_1& {\mathbf{a}}_2\\ |& |\end{array}\right]=\left[\begin{array}{c}-{\mathbf{a}}_1^{\ast }-\\ -{\mathbf{a}}_2^{\ast }-\\ -{\mathbf{a}}_3^{\ast }-\end{array}\right]$$

在这里, 列向量被标记为粗体${\mathbf{a}}_1$。行向量则有一个$\ast$号, 标记为${\mathbf{a}}_1^{\ast }$。转置向量和矩阵则用$\mathrm{T}$标记为${\mathbf{a}}^{\mathrm{T}}$和$A^{\mathrm{T}}$。

2、向量乘以向量——2个视角

后文中, 我将介绍一些概念, 同时列出“Linear Algebra for Everyone”一书中的相应部分 (部分编号插入如下)。详细的内容最好看书, 这里我也添加了一个简短的解释, 以便您可以通过这篇文章尽可能多地理解。

此外, 每个图都有一个简短的名称, 例如 v1 (数字 1 表示向量的乘积)、Mv1 (数字 1 表示矩阵和向量的乘积), 以及如下图 (v1) 所示的彩色圆圈。 如你所见, 随着讨论的进行, 该名称将被交叉引用。

• 1.1节 (p.2) Linear combination and dot products
• 1.3节 (p.25) Matrix of Rank One
• 1.4节 (p.29) Row way and column way

图 2: 向量乘以向量 - (v1), (v2)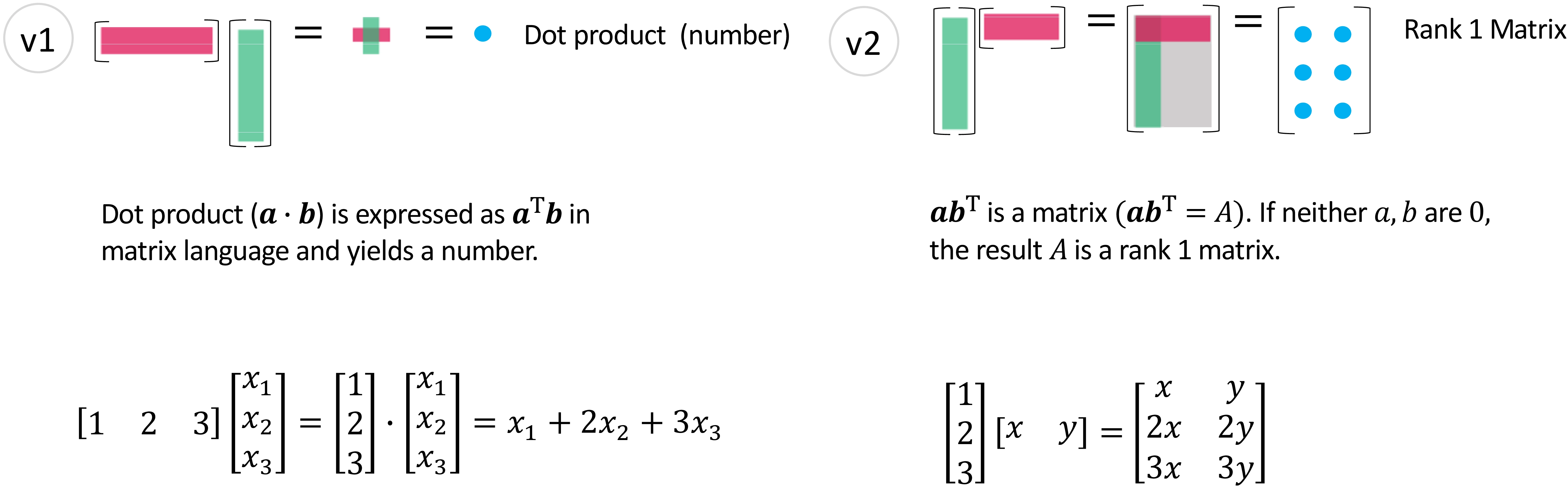

(v1) 是两个向量之间的基础运算, 而 (v2) 将列乘以行并产生一个秩1矩阵。理解 (v2) 的结果 (秩1) 是接下来章节的关键。

3、矩阵乘以向量——2个视角

一个矩阵乘以一个向量将产生三个点积组成的向量 (Mv1) 和一种$A$的列向量的线性组合。

• 1.1节 (p.3) Linear combinations
• 1.3节 (p.21) Matrices and Column Spaces

图 3: 矩阵乘以向量- (Mv1), (Mv2)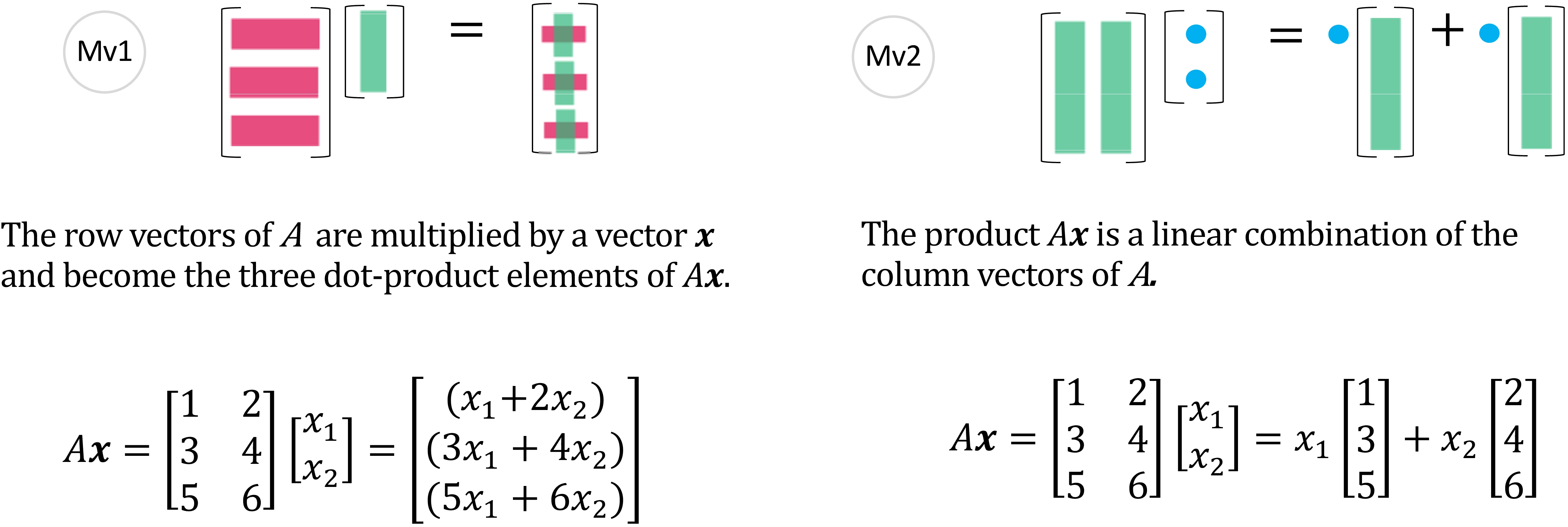

往往你会先学习 (Mv1). 但当你习惯了从 (Mv2) 的视角看待它, 会理解$A\mathbf{x}$是$A$的列的线性组合。矩阵$A$的列向量的所有线性组合生成的子空间记为$\mathbf{C}(A)$。$A\mathbf{x}=0$的解空间则是零空间, 记为$\mathbf{N}(A)$。

同理, 由 (vM1) 和 (vM2) 可见, 行向量乘以矩阵也是同一种理解方式。

图 4: 向量乘以矩阵 - (vM1), (vM2)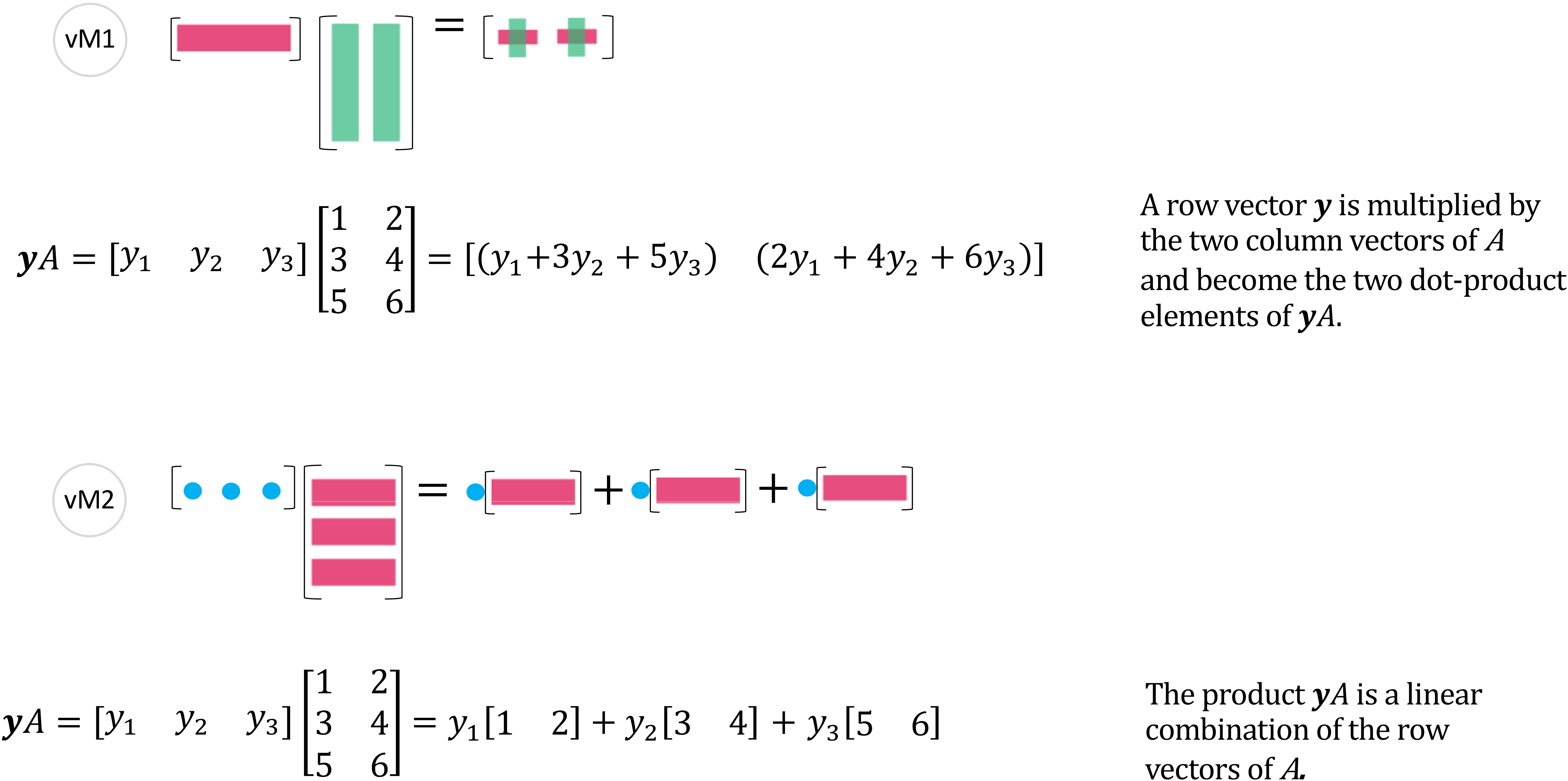

上图$A$的行向量的所有线性组合生成的子空间记为$\mathbf{C}(A^{\mathrm{T}})$。$yA=0$的解空间是$A$的左零空间, 记为 $\mathbf{N}(A^{\mathrm{T}})$。

本书的一大亮点即为四个基本子空间: 在${\mathbb{R}}^n$ 上的$\mathbf{N}(A)$ + $\mathbf{C}(A^{\mathrm{T}})$ (相互正交) 和在${\mathbb{R}}^m$ 上的$\mathbf{N}(A^{\mathrm{T}})$ + $\mathbf{C}(A)$ (相互正交)。

• 3.5节 (p.124) Dimensions of the Four Subspaces

图 5: 四个子空间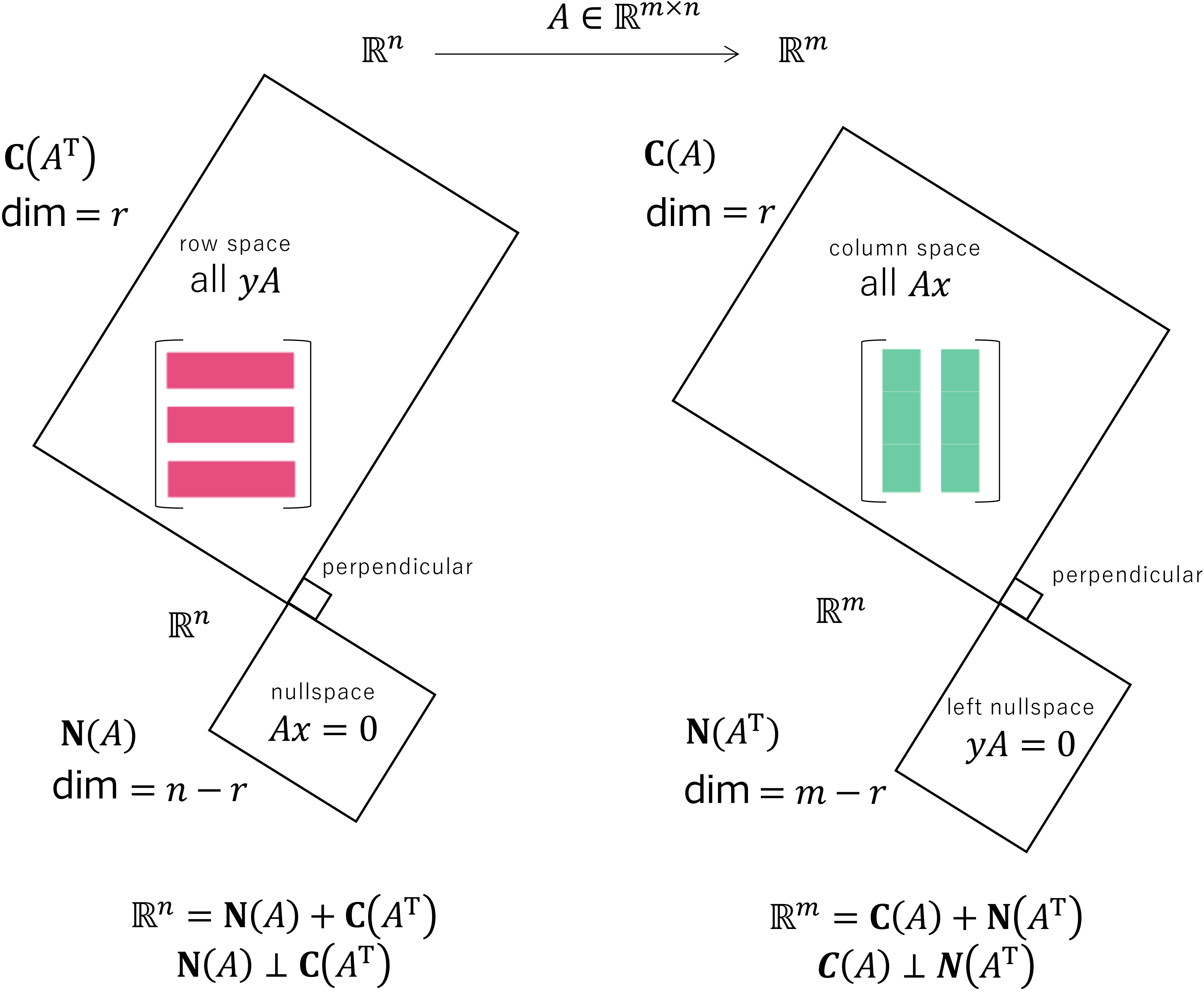

关于秩$r$, 请见$A=CR$ (6.1节)。

4、矩阵乘以矩阵——4个视角

由矩阵乘以向量"自然延伸到矩阵乘以矩阵"。

• 1.4节 (p.35) Four ways to multiply $\mathbf{AB}=\mathbf{C}$
• 也可以见书的封底

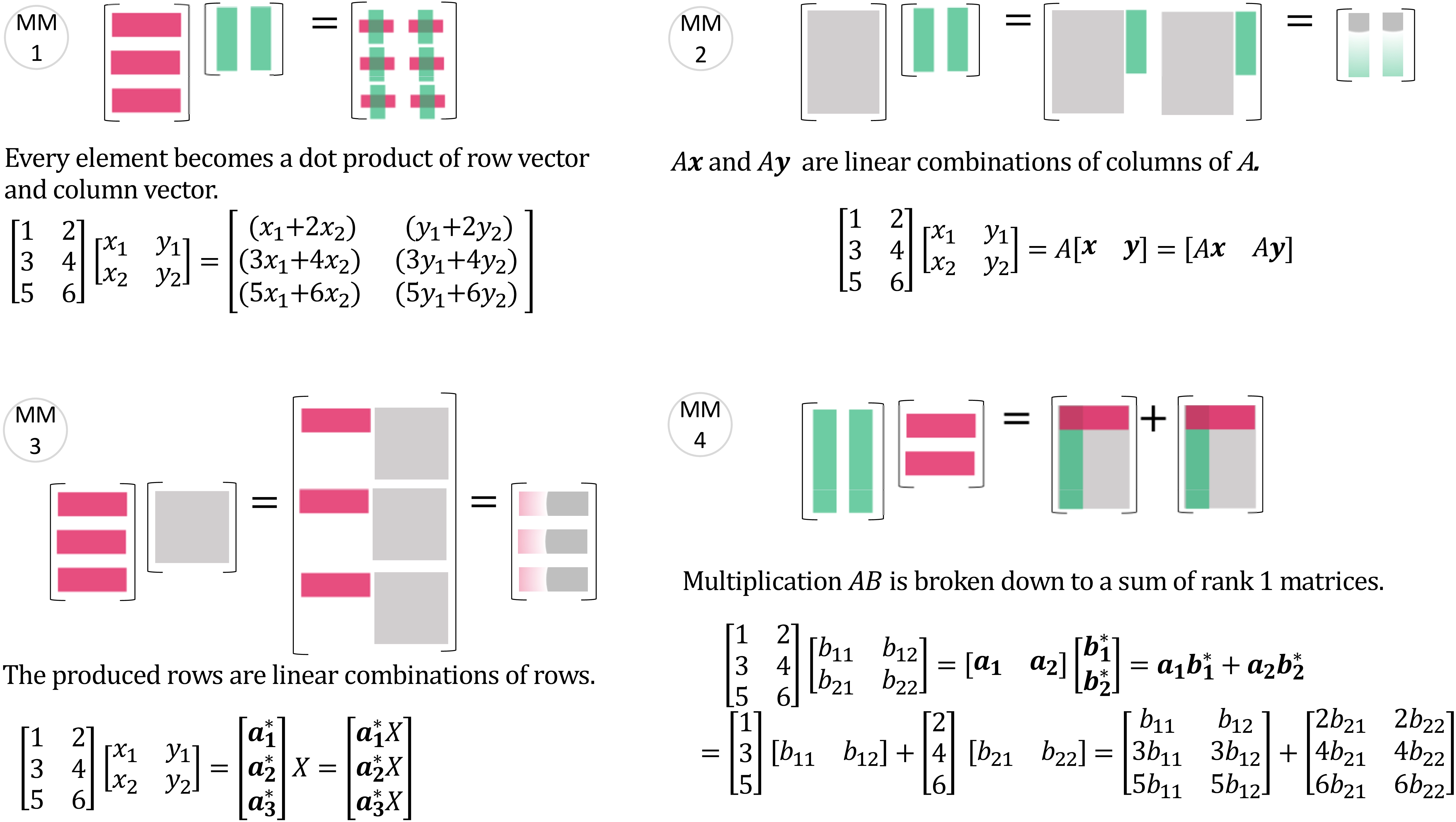
图 6: 矩阵乘以矩阵 - (MM1), (MM2), (MM3), (MM4)

5、实用模式

在这里, 我展示了一些实用的模式, 可以让你更直观地理解接下来的内容。

图 7: 图 1, 2 - (P1), (P1)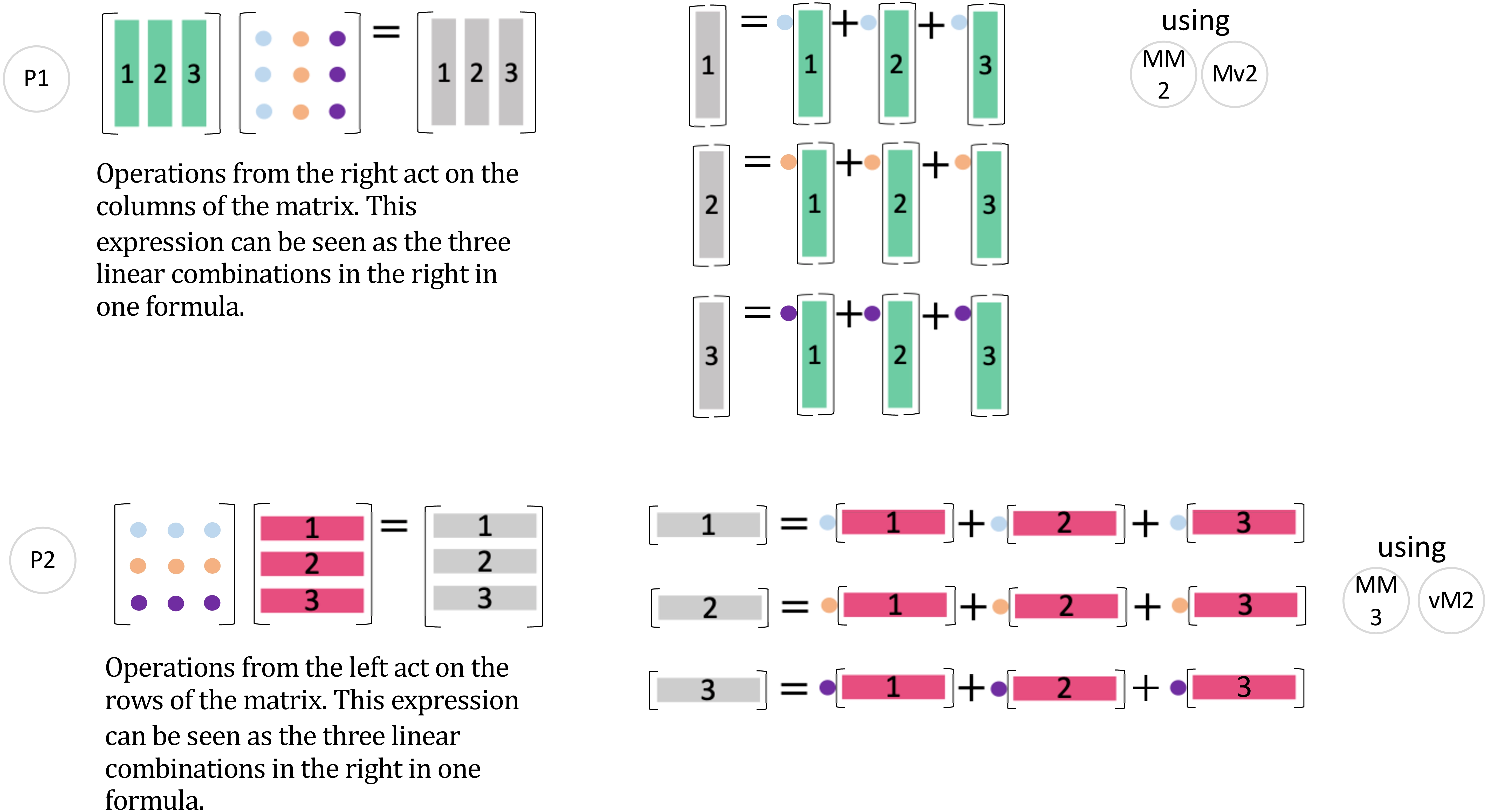

P1 是 (MM2) 和 (Mv2) 的结合。P2 是 (MM3) 和 (vM2) 的扩展。注意, P1 是列运算 (右乘一个矩阵), 而 P2 是行运算 (左乘一个矩阵)。

图 8: 图 1′, 2′ - (P1′), (P2′)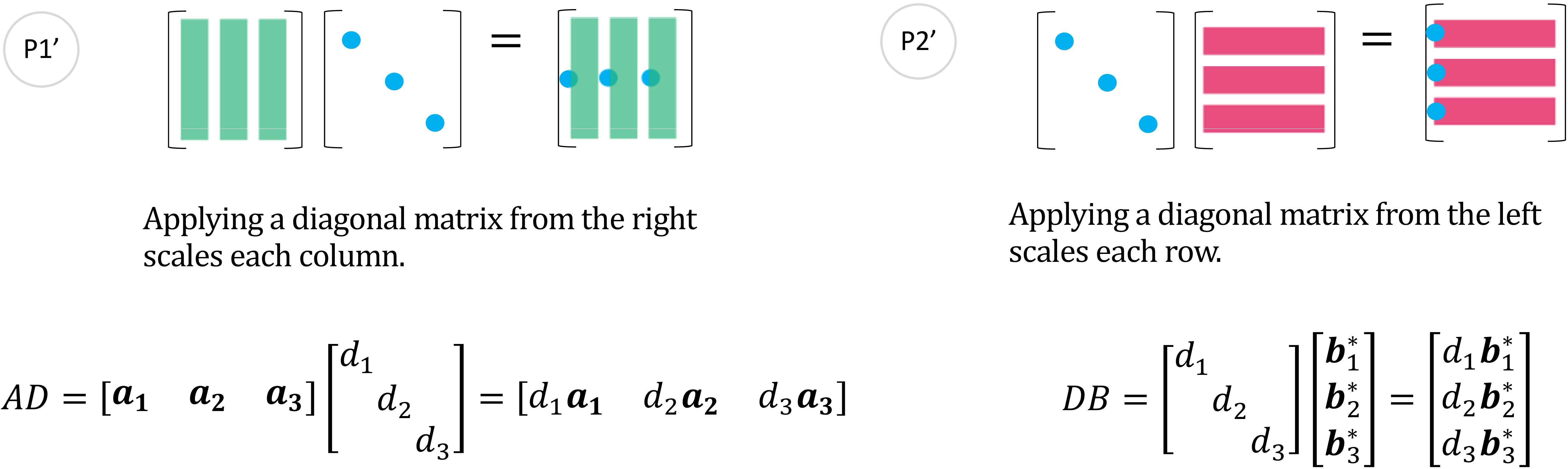

(P1′) 将对角线上的数乘以矩阵的列, 而 (P2′) 将对角线上的数乘以矩阵的行。两个分别为 (P1) 和 (P2) 的变体。

图 9: 图 3 - (P3)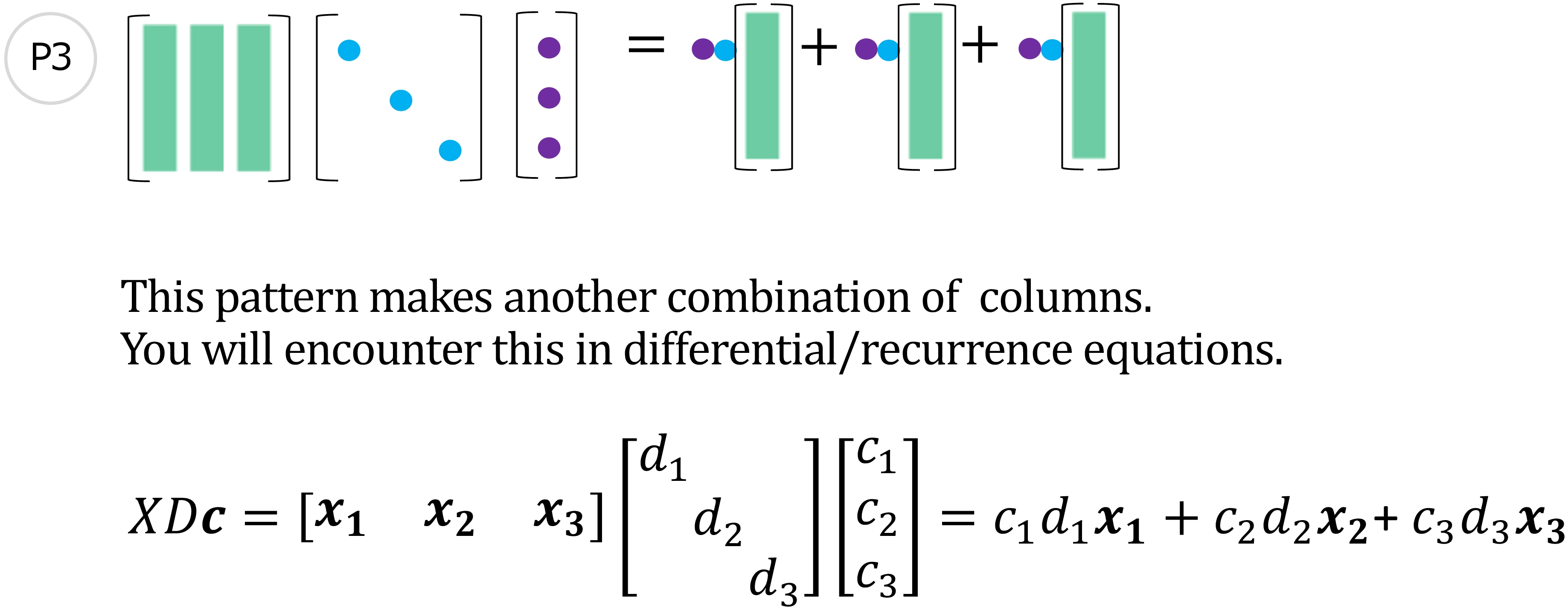

当解决微分方程和递归方程时的也会出现这一模式:

• 6节 (p.201) Eigenvalues and Eigenvectors
• 6.4节 (p.243) Systems of Differential Equations

$$\begin{array}{rl}\frac{d\mathbf{u}(t)}{dt}& =A\mathbf{u}(t),\mathbf{u}(0)={\mathbf{u}}_0\\ {\mathbf{u}}_{n+1}& =A{\mathbf{u}}_n,{\mathbf{u}}_0={\mathbf{u}}_0\end{array}$$

在两种问题中, 它的解都可以用$A$的特征值(${\lambda }_1,{\lambda }_2,{\lambda }_3$)、特征向量$X=\left[\begin{array}{ccc}{\mathbf{x}}_1& {\mathbf{x}}_2& {\mathbf{x}}_3\end{array}\right]$和系数$c={\left[\begin{array}{ccc}{c}_1& c_2& c_3\end{array}\right]}^{\mathrm{T}}$表示。其中$C$是以$X$为基底的初始值$\mathbf{u}(0)={\mathbf{u}}_0$的坐标。

$${\mathbf{u}}_0=c_1{\mathbf{x}}_1+c_2{\mathbf{x}}_2+c_3{\mathbf{x}}_3$$

$$\mathbf{c}=\left[\begin{array}{c}{c}_1\\ c_2\\ c_3\end{array}\right]=X^{-1}{\mathbf{u}}_0$$

以上两个问题的通解为:

$$\begin{array}{rlrl}\mathbf{u}(t)& =e^{At}{\mathbf{u}}_0=X{e}^{\Lambda t}{X}^{-1}{\mathbf{u}}_0& =X{e}^{\Lambda t}\mathbf{c}& =c_1{e}^{{\lambda }_{1}t}{\mathbf{x}}_1+c_2{e}^{{\lambda }_{2}t}{\mathbf{x}}_2+c_3{e}^{{\lambda }_{3}t}{\mathbf{x}}_3\\ {\mathbf{u}}_n& =A^n{\mathbf{u}}_0=X{\Lambda }^n{X}^{-1}{\mathbf{u}}_0& =X{\Lambda }^n\mathbf{c}& =c_1{\lambda }_1^n{\mathbf{x}}_1+c_2{\lambda }_2^n{\mathbf{x}}_2+c_3{\lambda }_3^n{\mathbf{x}}_3\end{array}$$

见图 9: 通过P3可以得到$XDc$​。

图 10: Pattern 4 - (P4)

P4在特征值分解和特异值分解中都会用到。两种分解都可以表示为三个矩阵之积, 其中中间的矩阵均为对角矩阵。且都可以表示为带特征值/特异值系数的秩1矩阵之积。

更多细节将在下一节中讨论。

6、矩阵的五种分解

• 前言 p.vii, The Plan for the Book.

$A=CR,A=LU,A=QR,A=Q\Lambda Q^{\mathrm{T}},A=U\Sigma V^{\mathrm{T}}$ 将一一说明。

分解	图示	说明
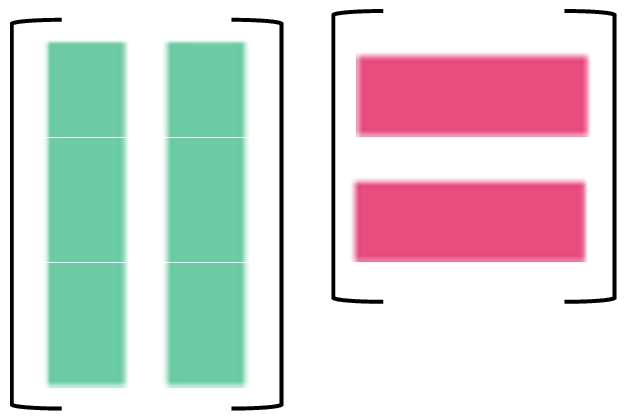$\mathbf{A}=\mathbf{CR}$		$C$为$A$的线性无关列 $R$为$A$的行阶梯形矩阵 可推知 列秩 = 行秩
$\mathbf{A}=\mathbf{LU}$		$LU$分解通过 高斯消去法 (下三角)(上三角)
$\mathbf{A}=\mathbf{QR}$		$QR$分解为 格拉姆-施密特正交化中的 正交矩阵$Q$和三角矩阵$R$
$\mathbf{S}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\mathrm{T}}$		对称矩阵$S$可以进行 特征值分解 特征向量组成$Q$, 特征值组成$\Lambda$
$\mathbf{A}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}$		所有矩阵$A$的 奇异值分解 奇异值组成$\Sigma$

表 1: 五种分解

6.1 $\mathbf{A}=\mathbf{CR}$

• 1.4节 Matrix Multiplication and $\mathbf{A}=\mathbf{CR}$ (p.29)

所有一般的长矩阵$A$都有相同的行秩和列秩。这个分解是理解这一定理最直观的方法。$C$由$A$的线性无关列组成, $R$为$A$的行阶梯形矩阵 (消除了零行)。$A=CR$将$A$化简为$r$的线性无关列$C$和线性无关行$R$的乘积。

$$\begin{array}{rl}A& =CR\\ \left[\begin{array}{ccc}1& 2& 3\\ 2& 3& 5\end{array}\right]& =\left[\begin{array}{cc}1& 2\\ 2& 3\end{array}\right]\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\end{array}\right]\end{array}$$

推导过程: 从左往右看$A$的列. 保留其中线性无关的列, 去掉可以由前者线性表出的列。则第1、2列被保留, 而第三列因为可以由前两列之和表示而被去掉。而要通过线性无关的1、2两列重新构造出$A$, 需要右乘一个行阶梯矩阵$R$。

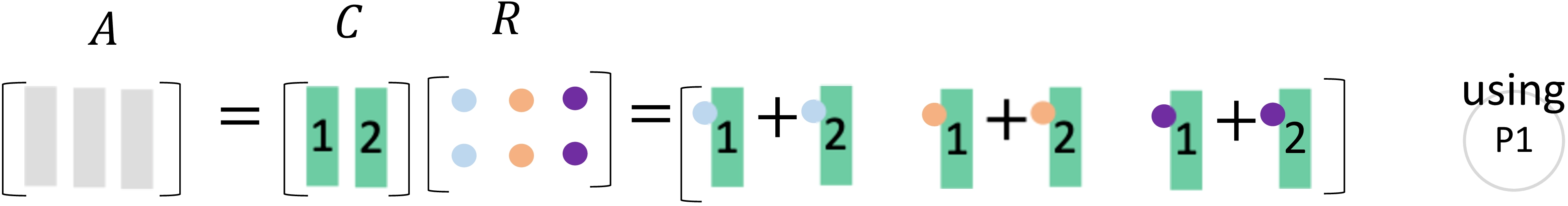
图 11: CR中列的秩

现在你会发现列的秩为2, 因为$C$中只有2个线性无关列。而$A$中所有的列都可以由$C$中的2列线性表出。

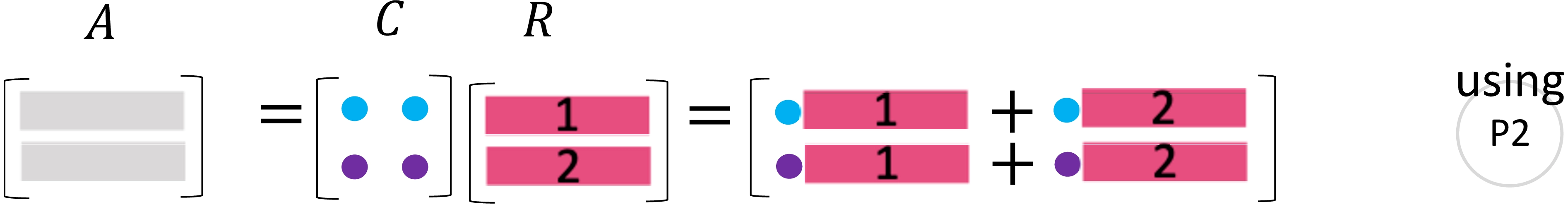
图 12: CR中行的秩

同样, 行秩也为2, 因为$R$中只有2个线性无关行, 且$A$中所有的行都可以由$R$中的2行线性表出。

6.2 $\mathbf{A}=\mathbf{LU}$

用高斯消除法求解$A\mathbf{x}=\mathbf{b}$也被称为$LU$分解。通常, 是$A$左乘一个初等行变换矩阵($E$)来得到一个上三角矩阵$U$。

$$\begin{array}{rl}EA& =U\\ A& =E^{-1}U\\ \text{let}L=E^{-1},A& =LU\end{array}$$

现在, 求解$A\mathbf{x}=\mathbf{b}$有2步: (1)求解$L\mathbf{c}=\mathbf{b}$, (2)代回$U\mathbf{x}=\mathbf{c}$。

• 2.3节 (p.57) Matrix Computations and $\mathbf{A}=\mathbf{LU}$

在这里, 我们直接通过$A$计算$L$和$U$。

$$A=\left[\begin{array}{c}|\\ {\mathbf{l}}_1\\ |\end{array}\right]\left[\begin{array}{c}-{\mathbf{u}}_1^{\ast }-\end{array}\right]+\left[\begin{array}{cc}0& \begin{array}{cc}0& 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}& A_2\end{array}\right]=\left[\begin{array}{c}|\\ {\mathbf{l}}_1\\ |\end{array}\right]\left[\begin{array}{c}-{\mathbf{u}}_1^{\ast }-\end{array}\right]+\left[\begin{array}{c}|\\ {\mathbf{l}}_2\\ |\end{array}\right]\left[\begin{array}{c}-{\mathbf{u}}_2^{\ast }-\end{array}\right]+\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& A_3\end{array}\right]=LU$$

图 13: $A$的递归秩1矩阵分离

要计算$L$和$U$, 首先分离出由$A$的第一行和第一列组成的外积。余下的部分为$A_2$。递归执行此操作, 将$A$分解为秩1矩阵之和。

图 14: 由$LU$重新构造$A$

由$L$乘以$U$来重新构造$A$则相对简单。

6.3$\mathbf{A}=\mathbf{QR}$

$A=QR$是在保持$\mathbf{C}(A)=\mathbf{C}(Q)$的条件下, 将$A$转化为正交矩阵$Q$。

• 4.4节 Orthogonal matrices and Gram-Schmidt (p.165)

在格拉姆-施密特正交化中, 首先, 单位化的${\mathbf{a}}_1$被用作${\mathbf{q}}_1$, 然后求出${\mathbf{a}}_2$与${\mathbf{q}}_1$正交所得到的${\mathbf{q}}_2$, 以此类推。

$$\begin{array}{rl}{\mathbf{q}}_1& ={\mathbf{a}}_1/||{\mathbf{a}}_1||\\ {\mathbf{q}}_2& ={\mathbf{a}}_2-({\mathbf{q}}_1^{\mathrm{T}}{\mathbf{a}}_2){\mathbf{q}}_1,{\mathbf{q}}_2={\mathbf{q}}_2/||{\mathbf{q}}_2||\\ {\mathbf{q}}_3& ={\mathbf{a}}_3-({\mathbf{q}}_1^{\mathrm{T}}{\mathbf{a}}_3){\mathbf{q}}_1-({\mathbf{q}}_2^{\mathrm{T}}{\mathbf{a}}_3){\mathbf{q}}_2,{\mathbf{q}}_3={\mathbf{q}}_3/||{\mathbf{q}}_3||\end{array}$$

或者你也可以写作$r_{ij}={\mathbf{q}}_i^{\mathrm{T}}{\mathbf{a}}_j$:

$$\begin{array}{rl}{\mathbf{a}}_1& =r_{11}{\mathbf{q}}_1\\ {\mathbf{a}}_2& =r_{12}{\mathbf{q}}_1+r_{22}{\mathbf{q}}_2\\ {\mathbf{a}}_3& =r_{13}{\mathbf{q}}_1+r_{23}{\mathbf{q}}_2+r_{33}{\mathbf{q}}_3\end{array}$$

原本的$A$就可以表示为$QR$: 正交矩阵乘以上三角矩阵。

$$\begin{array}{c}A=\left[\begin{array}{ccc}|& |& |\\ {\mathbf{q}}_1& {\mathbf{q}}_2& {\mathbf{q}}_3\\ |& |& |\end{array}\right]\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ & r_{22}& r_{23}\\ & & r_{33}\end{array}\right]=QR\\ \\ Q{Q}^{\mathrm{T}}=Q^{\mathrm{T}}Q=I\end{array}$$

图 15: $A=QR$

$A$的列向量就可以转化为一个正交集合: $Q$的列向量。$A$的每一个列向量都可以用$Q$和上三角矩阵$R$重新构造出。

图释可以回头看P1。

6.4 $\mathbf{S}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\mathrm{T}}$

所有对称矩阵$S$都必须有实特征值和正交特征向量。特征值是$\Lambda$的对角元素, 特征向量在$Q$中。

• 6.3节 (p.227) Symmetric Positive Definite Matrices

$$\begin{array}{rl}S=Q\Lambda Q^{\mathrm{T}}& =\left[\begin{array}{ccc}|& |& |\\ {\mathbf{q}}_1& {\mathbf{q}}_2& {\mathbf{q}}_3\\ |& |& |\end{array}\right]\left[\begin{array}{ccc}{\lambda }_1& & \\ & {\lambda }_2& \\ & & {\lambda }_3\end{array}\right]\left[\begin{array}{c}-{\mathbf{q}}_1^{\mathrm{T}}-\\ -{\mathbf{q}}_2^{\mathrm{T}}-\\ -{\mathbf{q}}_3^{\mathrm{T}}-\end{array}\right]\\ & \\ & ={\lambda }_1\left[\begin{array}{c}|\\ {\mathbf{q}}_1\\ |\end{array}\right]\left[\begin{array}{c}-{\mathbf{q}}_1^{\mathrm{T}}-\end{array}\right]+{\lambda }_2\left[\begin{array}{c}|\\ {\mathbf{q}}_2\\ |\end{array}\right]\left[\begin{array}{c}-{\mathbf{q}}_2^{\mathrm{T}}-\end{array}\right]+{\lambda }_3\left[\begin{array}{c}|\\ {\mathbf{q}}_3\\ |\end{array}\right]\left[\begin{array}{c}-{\mathbf{q}}_3^{\mathrm{T}}-\end{array}\right]\\ & ={\lambda }_1{P}_1+{\lambda }_2{P}_2+{\lambda }_3{P}_3\end{array}$$

$$P_1={\mathbf{q}}_1{\mathbf{q}}_1^{\mathrm{T}},P_2={\mathbf{q}}_2{\mathbf{q}}_2^{\mathrm{T}},P_3={\mathbf{q}}_3{\mathbf{q}}_3^{\mathrm{T}}$$

图 16: $S=Q\Lambda Q^{\mathrm{T}}$

一个对称矩阵$S$通过一个正交矩阵$Q$和它的转置矩阵, 对角化为$\Lambda$。然后被分解为秩一投影矩阵$P=q{q}^{\mathrm{T}}$的组合。这就是谱定理。

注意, 这里的分解用到了P4。

$$\begin{array}{c}S=S^{\mathrm{T}}={\lambda }_1{P}_1+{\lambda }_2{P}_2+{\lambda }_3{P}_3\\ Q{Q}^{\mathrm{T}}=P_1+P_2+P_3=I\\ P_1{P}_2=P_2{P}_3=P_3{P}_1=O\\ P_1^2=P_1=P_1^{\mathrm{T}},P_2^2=P_2=P_2^{\mathrm{T}},P_3^2=P_3=P_3^{\mathrm{T}}\end{array}$$

6.5 $\mathbf{A}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}$

• 7.1节 (p.259) Singular Values and Singular Vecrtors

包括长方阵在内的所有矩阵都具有奇异值分解(SVD)。$A=U\Sigma V^{\mathrm{T}}$中, 有$A$的奇异向量$U$和$V$。奇异值则排列在$\Sigma$的对角线上。下图就是“简化版”的SVD。

图 17: $A=U\Sigma V^{\mathrm{T}}$

你可以发现, $V$是${\mathbb{R}}^n$ ($A^{\mathrm{T}}A$的特征向量) 的标准正交基, 而$U$是 ${\mathbb{R}}^m$ ($A{A}^{\mathrm{T}}$的特征向量) 的标准正交基。它们共同将$A$对角化为$\Sigma$。这也可以表示为秩1矩阵的线性组合。

$$\begin{array}{rlr}A=U\Sigma V^{\mathrm{T}}& =\left[\begin{array}{ccc}|& |& |\\ {\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\\ |& |& |\end{array}\right]\left[\begin{array}{ccc}{\sigma }_1& & \\ & {\sigma }_2& \\ & & \end{array}\right]\left[\begin{array}{c}-{\mathbf{v}}_1^{\mathrm{T}}-\\ -{\mathbf{v}}_2^{\mathrm{T}}-\end{array}\right]& ={\sigma }_1\left[\begin{array}{c}|\\ {\mathbf{u}}_1\\ |\end{array}\right]\left[\begin{array}{c}-{\mathbf{v}}_1^{\mathrm{T}}-\end{array}\right]+{\sigma }_2\left[\begin{array}{c}|\\ {\mathbf{u}}_2\\ |\end{array}\right]\left[\begin{array}{c}-{\mathbf{v}}_2^{\mathrm{T}}-\end{array}\right]\\ & ={\sigma }_1{\mathbf{u}}_1{\mathbf{v}}_1^{\mathrm{T}}+{\sigma }_2{\mathbf{u}}_2{\mathbf{v}}_2^{\mathrm{T}}& \end{array}$$

注意:

$$\begin{array}{rl}U{U}^{\mathrm{T}}& =I_m\\ V{V}^{\mathrm{T}}& =I_n\end{array}$$

图释见P4。

总结和致谢

我展示了矩阵/向量乘法的系统可视化与它们在五种矩阵分解中的应用。我希望你能够喜欢它们、通过它们加深对线性代数的理解。

Ashley Fernandes 在排版时帮我美化了这篇论文, 使它更加一致和专业。

在结束这篇论文之前, 我要感谢 Gilbert Strang 教授出版了《Linear Algebra for Everyone》一书。它引导我们通过新的视角去了解线性代数中这些美丽的风景。其中介绍了当代和传统的数据科学和机器学习, 每个人都可以通过实用的方式对它的基本思想进行基本理解。 矩阵世界的重要组成部分。

参考文献与相关工作

1. Gilbert Strang(2020), Linear Algebra for Everyone, Wellesley Cambridge Press.,http://math.mit.edu/everyone
2. Gilbert Strang(2016), Introduction to Linear Algebra, Wellesley Cambridge Press, 5th ed.,http://math.mit.edu/linearalgebra
3. Kenji Hiranabe(2021), Map of Eigenvalues, An Agile Way(blog),https://anagileway.com/2021/10/01/map-of-eigenvalues/

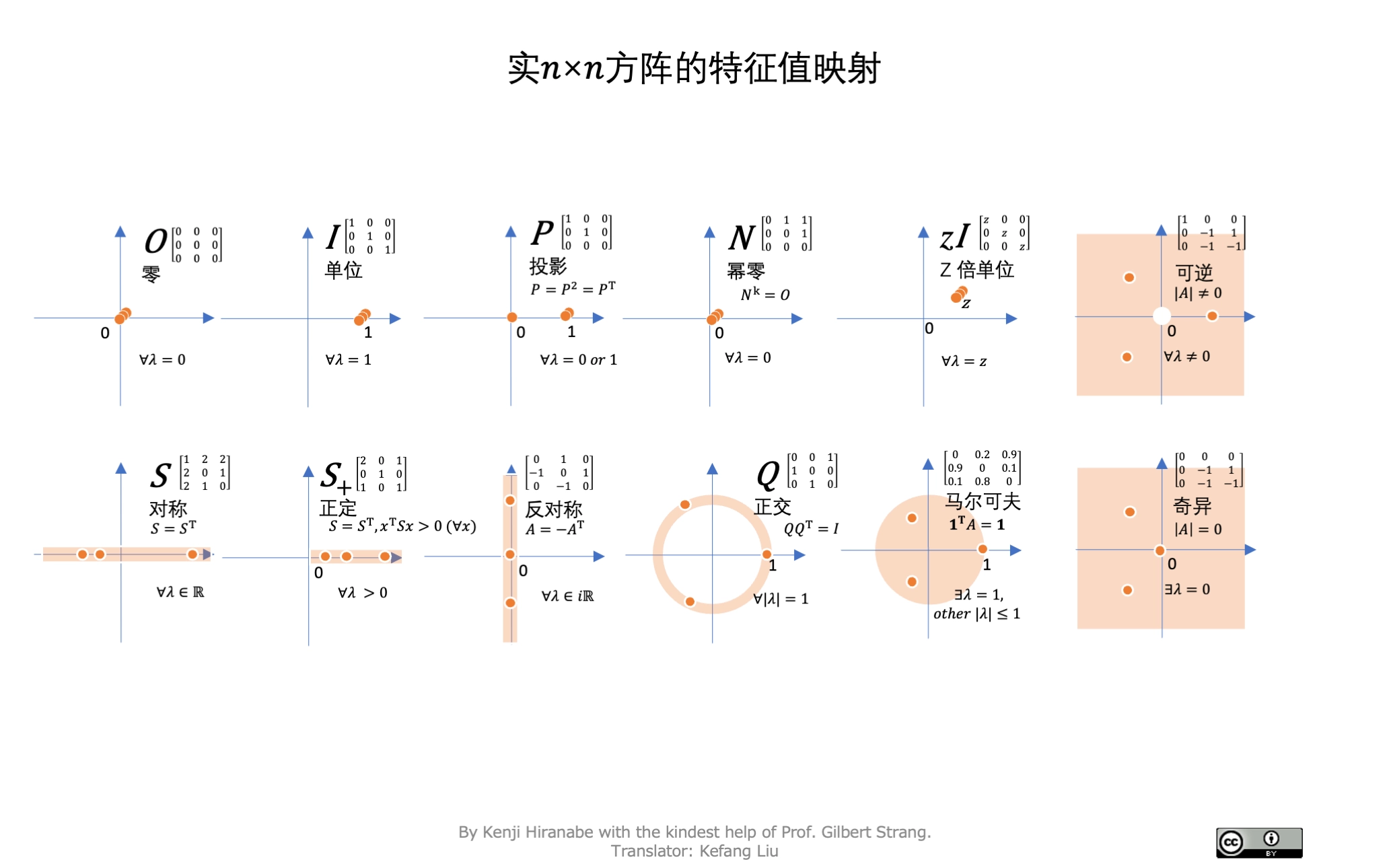
   图 18: 特征值图

4. Kenji Hiranabe(2020), Matrix World, An Agile Way(blog),\ https://anagileway.com/2020/09/29/matrix-world-in-linear-algebra-for-everyone/

   图 19: 矩阵世界

---

---

1. twitter: @hiranabe, [email protected], https://anagileway.com ↩︎

2. Massachusetts Institute of Technology, http://www-math.mit.edu/~gs/ ↩︎

3. twitter: @kfchliu, 微博用户: 5717297833 ↩︎

4. “Linear Algebra for Everyone": http://math.mit.edu/everyone/. ↩︎